In tldraw, we give our geometric shapes a hand-drawn style through intentionally designed imperfections. We find that subtle variations between generated shapes adds character, loosens up wireframes, and looks better alongside sketches drawn freehand.

Engineering imperfection in this way makes use of an interesting mechanism under the hood. Our space for variety needed to be narrow enough so each geometric shape was easily recognizable, but broad enough such that no two shapes looked exactly alike. Crucially, each shape's imperfections needed to be _stable_ and persist through resizing and transformation on the canvas.

In this article, we'll explore how tldraw uses (pseudo)randomness to achieve the hand-drawn look, and how we make the resulting variations stable across renders.

Random jittering

A first attempt at adding imperfection might just call Math.random() when rendering:

// Don't do this
const offset = { x: Math.random() * 3.14, y: Math.random() * 3.14 }

// Don't do this
const offset = { x: Math.random() * 3.14, y: Math.random() * 3.14 }

// Don't do this
const offset = { x: Math.random() * 3.14, y: Math.random() * 3.14 }

The problem is that this creates shapes that jitter on every render.

React re-renders whenever the shape's state changes. Each render produces new random numbers, which is why the subtle variations shift so quickly.

To avoid this jitter, we need each shape's rendering code to produce the same sequence of random numbers each time it renders.

We can achieve this with a pseudorandom number generator:

function rng(seed = '') {
    let x = 0
    let y = 0
    let z = 0
    let w = 0

    function next() {
        const t = x ^ (x << 11)
        x = y
        y = z
        z = w
        w ^= ((w >>> 19) ^ t ^ (t >>> 8)) >>> 0
        return (w / 0x100000000) * 2
    }

    for (let k = 0; k < seed.length + 64; k++) {
        x ^= seed.charCodeAt(k) | 0
        next()
    }

    return next
}

function rng(seed = '') {
    let x = 0
    let y = 0
    let z = 0
    let w = 0

    function next() {
        const t = x ^ (x << 11)
        x = y
        y = z
        z = w
        w ^= ((w >>> 19) ^ t ^ (t >>> 8)) >>> 0
        return (w / 0x100000000) * 2
    }

    for (let k = 0; k < seed.length + 64; k++) {
        x ^= seed.charCodeAt(k) | 0
        next()
    }

    return next
}

function rng(seed = '') {
    let x = 0
    let y = 0
    let z = 0
    let w = 0

    function next() {
        const t = x ^ (x << 11)
        x = y
        y = z
        z = w
        w ^= ((w >>> 19) ^ t ^ (t >>> 8)) >>> 0
        return (w / 0x100000000) * 2
    }

    for (let k = 0; k < seed.length + 64; k++) {
        x ^= seed.charCodeAt(k) | 0
        next()
    }

    return next
}

When you call this function with a particular seed, it will return a function which produces a new random number each time it's called. While each number is pseudo-random (i.e. close enough to random, but not close enough for your bank), if the seed is the same, then the numbers themselves will always come out in the same order.

Now that we have a method, all we need is a seed.

Stable variation

Since every shape has a unique and stable ID, we can use this ID as the seed for the generator.

You can actually see this in action by making a clone of a shape while dragging. You can click and drag a shape to move it on the canvas, but the moment you press the alt key, we move the dragging shape back to where it was and create a new shape under your cursor, and make this the dragging shape instead.

You can toggle the clone interaction to see the variation between the two shapes, each of which have different IDs, and so different random offsets.

Stroke texture

When drawing shapes with pen and paper, the lines themselves may vary in width according to the texture of the paper and the angle of your pen. While we go to great lengths to model this with our draw shape, we wanted to capture that effect with our geometric shapes, too.

To do this, we render each path multiple times, with each pass using slightly different random offsets. The trick is to modify the seed for each pass:

for (let pass = 0; pass < passes; pass++) {
   const random = rng(randomSeed + pass)
   // draw the path with this pass's random offsets
}

for (let pass = 0; pass < passes; pass++) {
   const random = rng(randomSeed + pass)
   // draw the path with this pass's random offsets
}

for (let pass = 0; pass < passes; pass++) {
   const random = rng(randomSeed + pass)
   // draw the path with this pass's random offsets
}

Varying the seed produces different random sequences, which leads to different offsets, but these multiple passes are also stable between renders so the randomness matches each time.

By default we render two passes. The result is a stroke that looks more like real ink; thicker and more textured than a single wobbly line.

Softening corners

Sharp corners are another giveaway that something was drawn by a computer. We soften them using quadratic bezier curves, and apply different rounding depending on the angle of the corner. A sharp 90° corner needs significant rounding to look hand-drawn, and a corner closer to 180° needs far less. This is to preserve the overall geometry of the shape.

const roundnessClampedForAngle = modulate(
   Math.abs(Vec.AngleBetween(tangentToPrev, tangentToNext)),
   [Math.PI / 2, Math.PI], // 90° to 180°
   [roundness, 0], // full roundness at 90°, none at 180°
   true
)

const roundnessClampedForAngle = modulate(
   Math.abs(Vec.AngleBetween(tangentToPrev, tangentToNext)),
   [Math.PI / 2, Math.PI], // 90° to 180°
   [roundness, 0], // full roundness at 90°, none at 180°
   true
)

const roundnessClampedForAngle = modulate(
   Math.abs(Vec.AngleBetween(tangentToPrev, tangentToNext)),
   [Math.PI / 2, Math.PI], // 90° to 180°
   [roundness, 0], // full roundness at 90°, none at 180°
   true
)

Tiny shapes

Finally, if a shape is resized and the width or height segments become very small, we don’t want the rounding to overlap or consume the entire segment. To prevent this, we clamp the rounding such that long segments aren’t affected but short segments get reduced rounding.

const roundnessBeforeClampedForLength = Math.min(
    roundnessClampedForAngle,
    (currentInfo?.length ?? Infinity) / 4
)
const roundnessAfterClampedForLength = Math.min(
    roundnessClampedForAngle,
    (nextInfo?.length ?? Infinity) / 4
)

const roundnessBeforeClampedForLength = Math.min(
    roundnessClampedForAngle,
    (currentInfo?.length ?? Infinity) / 4
)
const roundnessAfterClampedForLength = Math.min(
    roundnessClampedForAngle,
    (nextInfo?.length ?? Infinity) / 4
)

const roundnessBeforeClampedForLength = Math.min(
    roundnessClampedForAngle,
    (currentInfo?.length ?? Infinity) / 4
)
const roundnessAfterClampedForLength = Math.min(
    roundnessClampedForAngle,
    (nextInfo?.length ?? Infinity) / 4
)

This way, the rounded corners don’t eat up the entire shape:

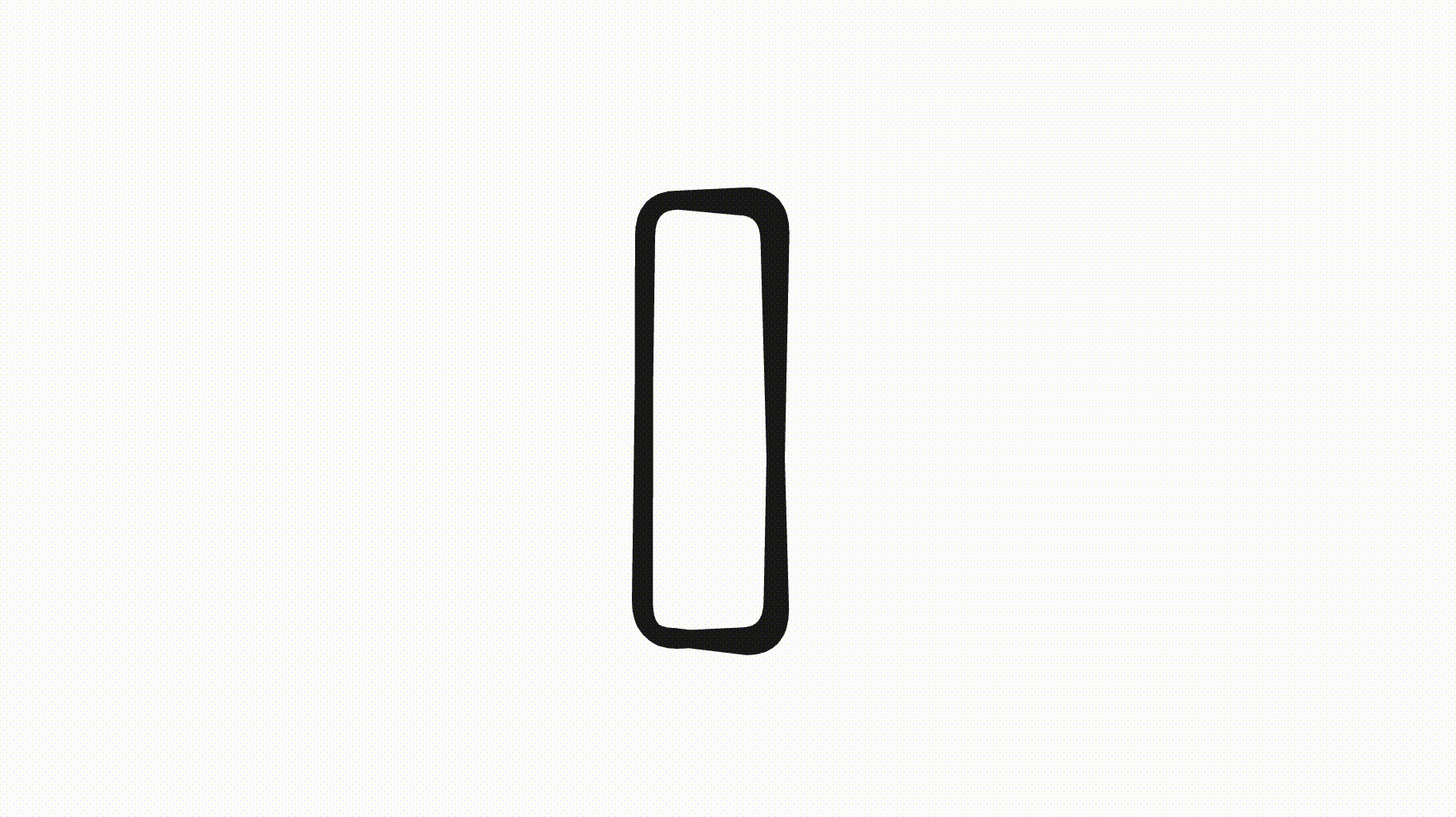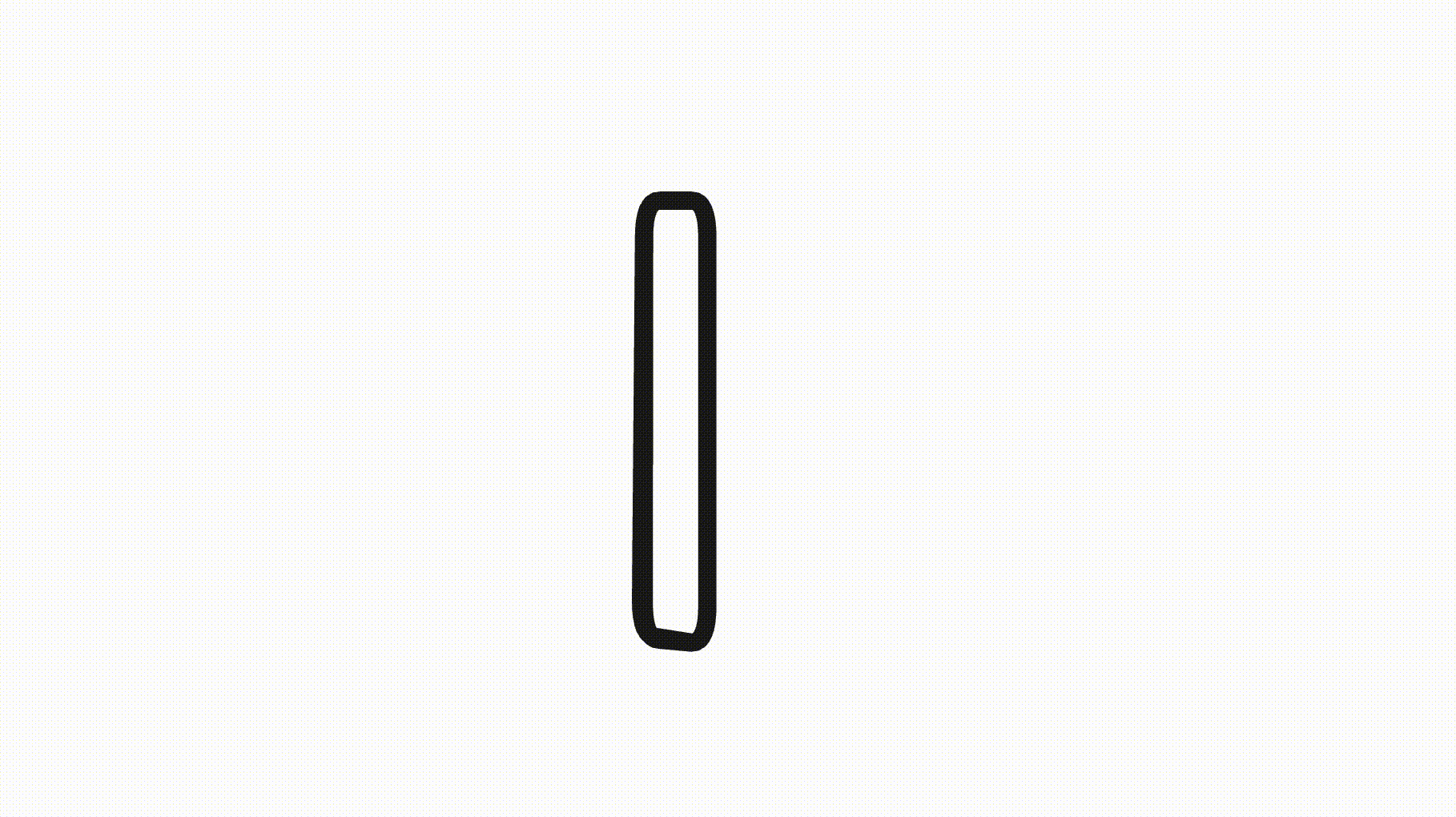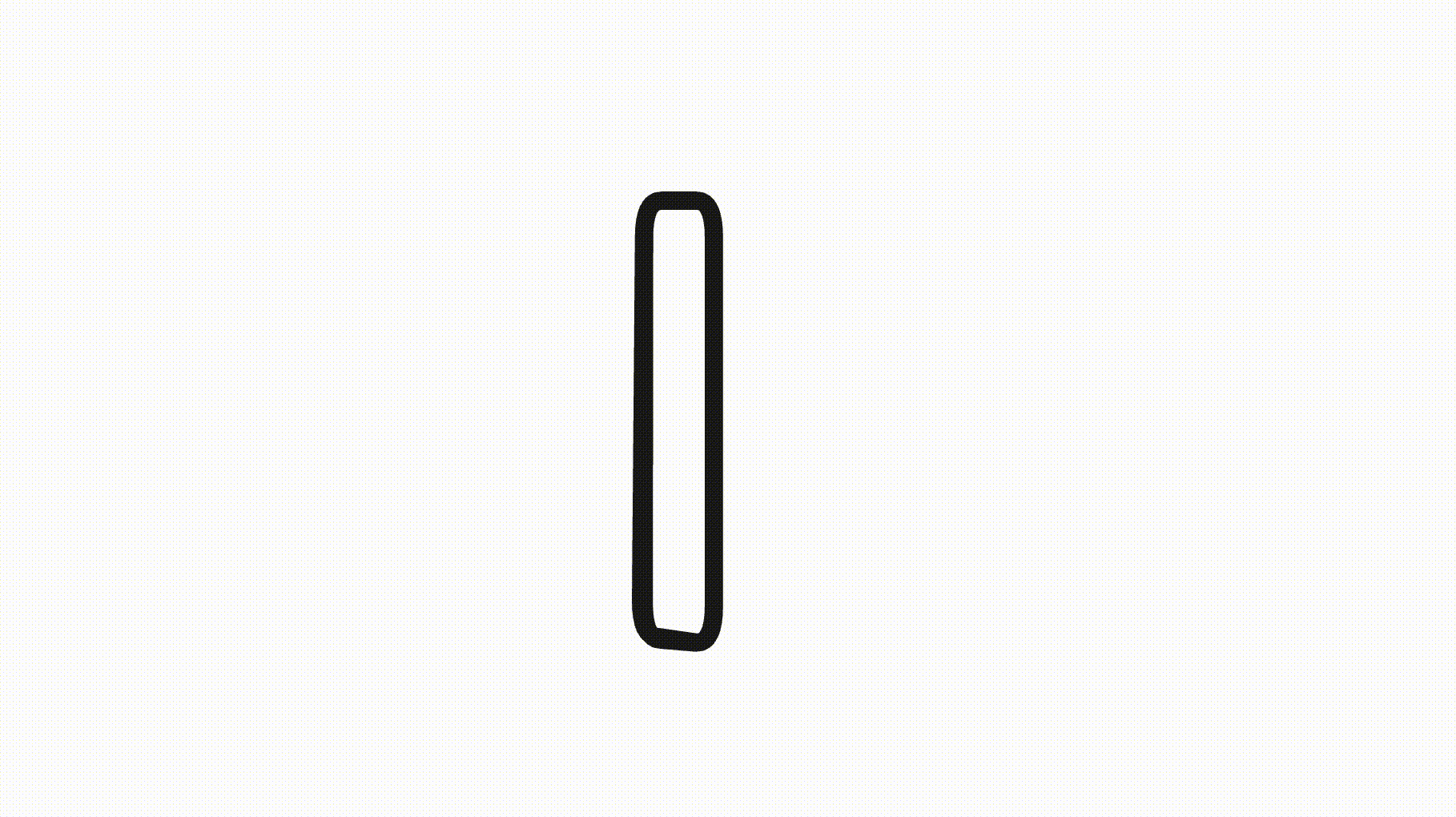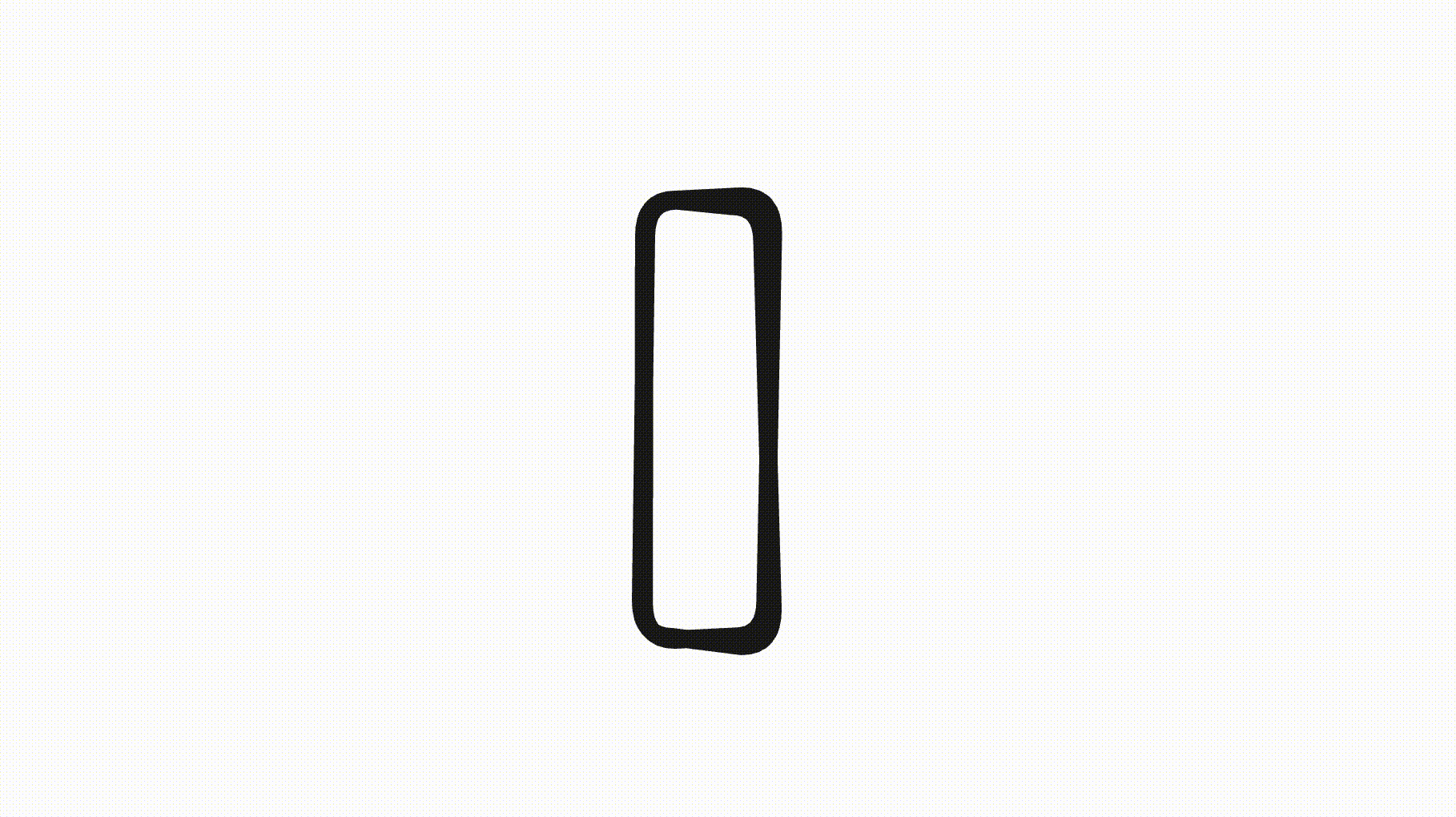
Future offsets

Funny enough, while writing this article we stumbled on a bug in the algorithm: because the offsets use a normalized x and y, the area of potential offset is square rather than circular.

// square field
const offset = { 
  x: random() * offsetAmount, 
  y: random() * offsetAmount 
}

// round field
const { x, y } = new Vec(random(), random()).mul(random() * offsetAmount)

// square field
const offset = { 
  x: random() * offsetAmount, 
  y: random() * offsetAmount 
}

// round field
const { x, y } = new Vec(random(), random()).mul(random() * offsetAmount)

// square field
const offset = { 
  x: random() * offsetAmount, 
  y: random() * offsetAmount 
}

// round field
const { x, y } = new Vec(random(), random()).mul(random() * offsetAmount)

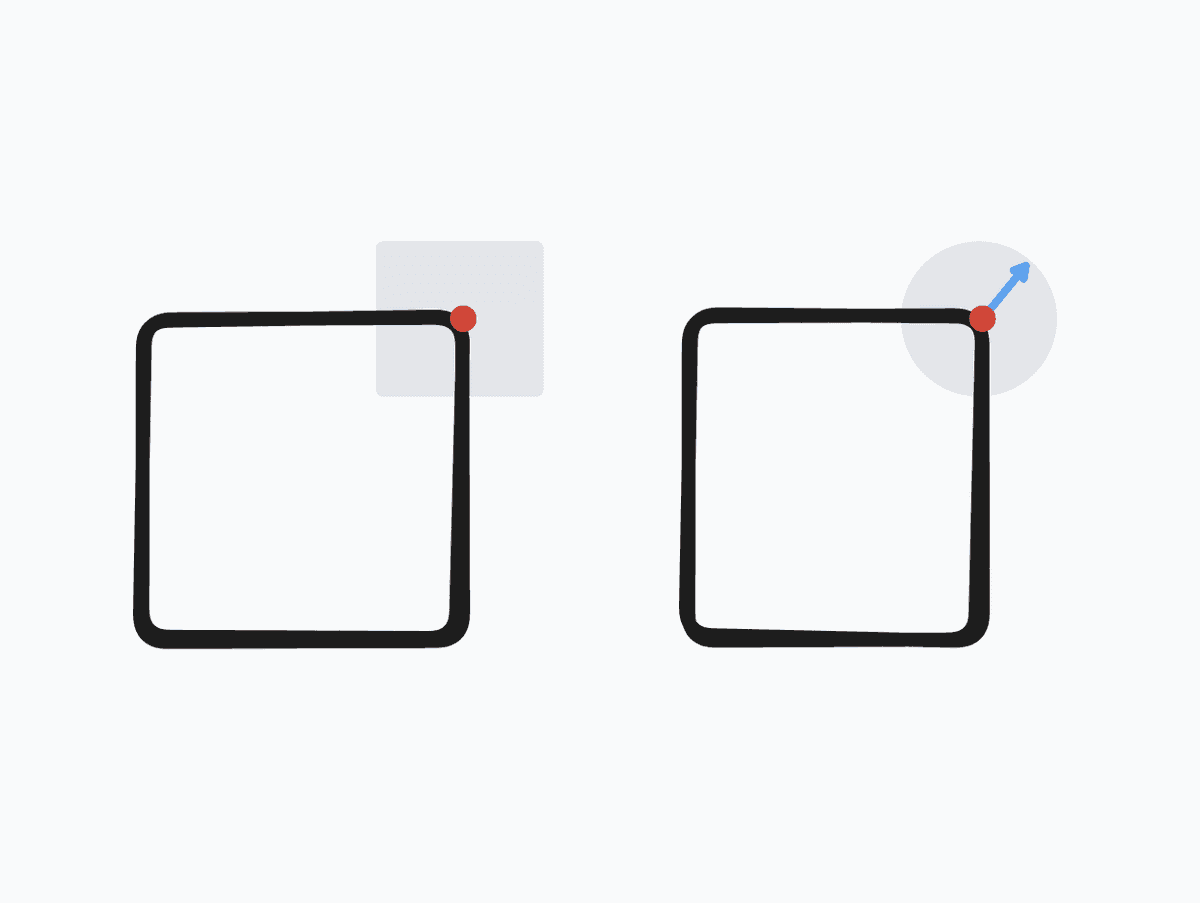
In the current implementation, points tend to the corners of the square field. A more beautiful alternative would be to use a random vector and magnitude, creating a round field of possible offsets.

Seems our randomness could be more imperfect still.